MU 207 Quiz Study Guide

Office hours 4:30 - 5:30 pm Tues

MacLaurin A177

Source materials:  CLASS NOTES, COURSEPACK

Introduction to acoustics. Hooke's law, SHM, vibrating spring vs. vibrating string, transverse vs longitudinal propogation of sound

Examples:

-What is the difference between transverse and longitudinal waves?

-What is the frequency of a single mass-spring system with respect to k, the spring constant, and m, the mass?

-What does a linear restoring force mean?

Sinusoids are uniquely determined by three characteristics: amplitude, frequency and phase.
Another way to represent frequency is the period T: T = 1/f or f = 1/T.

In addition, there is a physical dimension to a wave, which is its wavelength λ:   v = f λ or λ = v/f or f = v/λ

Examples:

-- what is the period of A440?

T = 1/f = 1/440 = 0.0023 secs (2.3 milliseconds)

-- what is the wavelength of A440?

v=f λ so λ = v/f = 343/440 = 0.78 meters

v = f λ so λ = v/f = 343/200,000 = 0.001715 meters, quite small

-- what is the frequency of sound with a 1 meter-long wavelength?

f = v/λ = 343/1 = 343 Hz

Know these terms: Harmonics, resonance, standing waves, difference between modes and nodes, reflections, linear superposition, constructive and destructive interference

Examples:

-- what is the frequency of the 12th harmonic of middle C?

261.63 * 12 = 3,139.56 Hz

440 * 100 = 44,000 Hz

--what are the modes of resonance of an open tube 1 meter long?

so the fundamental freq is 343/2 = 171.5 Hz (approximately)
and the harmonics (modes of resonance) are multples of that, so 2*171.5, 3*171.5, etc...

Fourier Theory, Time domain vs. frequency domain

-construction of a square wave from its harmonics

-additive synthesis (also called Fourier Synthesis)
-Fourier analysis, spectrum

The phsics and mathematics of intervals, tuning systems:  just, Pythagorean, meantone, equal tempered tunings, beats

Examples:

-Show that just intonation has two different sized whole steps:

We can look at the whole steps from C to D and from D to E.
The first whole-step is 9/8 ÷ 1 = 9/8
The next whole-stop is 5/4 ÷ 9/8 = 5/4 * 8/9 = 10/9, which is slightly smaller whole-step

-By how many cents do these two different whole steps differ?

1200log(9/8)/log2 = 203.91 cents vs 1200log(10/9)/log2 = 182.4 cents. The difference is 21.51 cents, around a fifth of a semitone.

The ratio for a just M3 = 5/4 and the ratio for a just m3 = 6/5
Adding intervals is the same as mulplying their ratios, so we get 5/4 * 6/5 = 6/4 = 3/2

READ: The Science of Musical Sound, Chapters 1-4

Reference Section (this material is not necessarily used)

• At room temperature (68° Fahrenheit), the velocity of sound in air is: 343 meters/second = 769 mph = 1,128 feet/second  = 769 miles/hour. 
In water  the speed of sound is: 1,497 meters/second.

       
where v is velocity, L is length of the string or air column, is the fundamental, is the nth harmonic

                                 
where v = velocity of a disturbance passing along a string, T is tension of the string, µ is mass per unit length (thickness)

                      
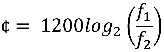
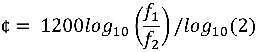
                                                                (if your calculator can't do log base 2)

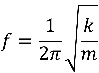
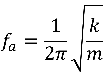
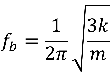
1¢ is defined as 1/100th of an equal-tempered semitone